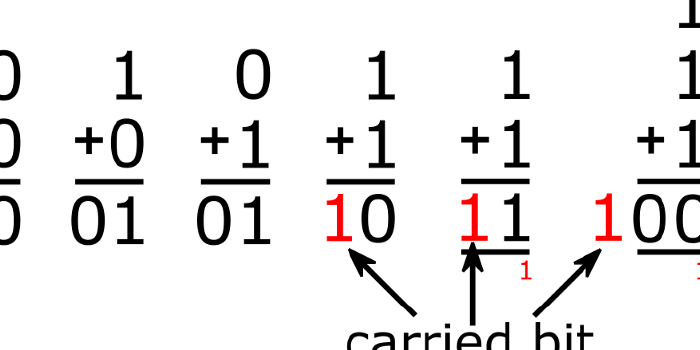Under The Bonnet: Floating Point

If you’re scientist, or doing anything with fraction and live in the world of binary.

Number Line. Credits By XKCD

We have talked about integers, characters and strings in the past two posts in this series. There is one more important type: number with fraction. This data type is so important for scientific, mathematical, or financial computation. This includes games, location-based applications, and data analysis.

In science we have enormous as well as minuscule constants. For example:

Speed of light in the vacuum 𝗖 is roughly 300,000,000,000 m/s.
𝛑 is roughly 3.14159
ℎ is 0.000000000000000000000000000000000662607004 m² kg/s

The number can be extremely large or extremely small. To simplify calculations, we use scientific notation. Therefore the Planck’s constant ℎ can be written as 6.62607004 × 10³⁴. Let’s examine how it works in decimal.

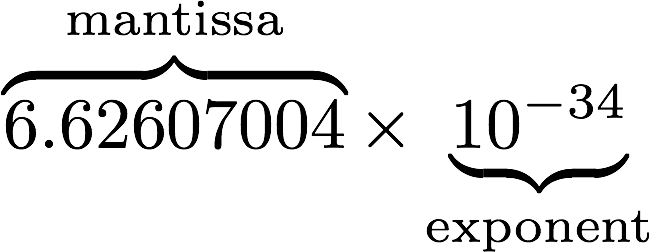
Scientific Notation

The first part is called mantissa. It’s the part of scientific notation with significant digits. The latter part is called exponent. This signify how many digit we need to move to the right if it is positive and to the left if it is negative.

Mantissa and exponent in binary.

Not dissimilar to integers, characters, and strings. Number with fraction is also represented in bits and bytes. The layout of representing them is standardised by IEEE 754.

The data type in Java for single and double precision floating number is float and double respectively. The float data type is 32-bit long and the double data type is 64-bit long. The standard does not dictate about the endianess, therefore I’ll just use MSB and LSB as marker and no address.

IEEE 754 single and double precision bit.

Binary fraction is the same with decimal. But instead of ¹⁄₁₀, ¹⁄₁₀₀ we go to ¹⁄₂, ¹⁄₄ and so on. Let’s say we have an arbitrary real number of 34.3125. Here’s how we find the representation

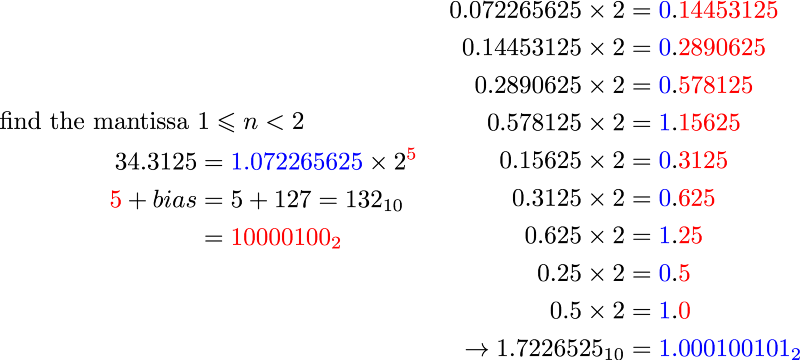
First, we need to find a value so that the mantissa is 1≤𝑛<2. If the absolute positive number is more than 1 we divide by 2, if it’s less than one, multiply them by two until we reach such number. In this case we found out that 34.3125 = 1.072265625 × 2⁵.

IEEE 754 decides that to represent exponent, we add some bias value. For 32-bit floating numbers it’s 127. Everything below 127 is negative exponent, and above 127 is positive exponent.

As for the mantissa, IEEE 754 decides to use sign-and-magnitude format. Because our number is positive, the sign bit is off. They also decide that it’s imperative to just remove the 1 from the mantissa. 1.000100101 is represented in the mantissa part as 000100101

Representing 34.3125 in IEEE-754 binary

The blocks below is how the byte array will be layout from the MSB to LSB. In the little endian, it goes from LSB to MSB. As for big endian it’s from MSB to LSB.

Test it in Go

We’ve used Python and Java in the past. Now, we’ll try golang. The purpose of using various languages is to show that it’s the same in all languages.

package main

import (  
 "bytes"  
 "encoding/binary"  
 "fmt"  
)

func main() {  
  const n float32 = 34.3125
  bufLE := new(bytes.Buffer)  
  binary.Write(bufLE, binary.LittleEndian, n)
  bufBE := new(bytes.Buffer)  
  binary.Write(bufBE, binary.BigEndian, n)`
  fmt.Printf("Representation of %.4f in\nLittle Endian\t: % x\nBig Endian\t: % x",  
  n, bufLE.Bytes(), bufBE.Bytes())  
}

The output is as expected

> go run main.go  
Representation of 34.3125 in  
Little Endian : 00 40 09 42  
Big Endian : 42 09 40 00

Precision Problem

The problem with floating point is it’s imprecise for fraction that is not multiple of 2-¹. It’s good enough for simulation or games. However, it poses a problem when we use them for cases like currency due to accumulation of the precision loss. Let me give you an example: 0.1 + 0.2. Intuitively it’s 0.3, but let compute them the way computer compute it.

The difference in exponent is 1. To add those we need to normalise to the biggest. So we shift the mantissa of 𝑥 by one bit to make xE = yE

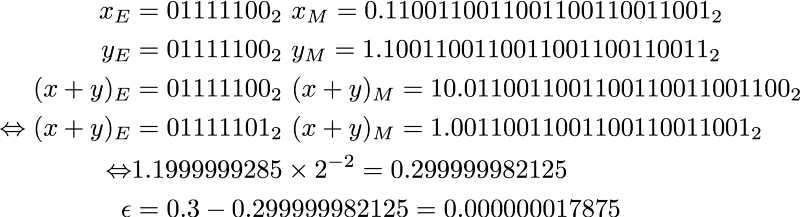
The final representation of the number is not exactly 0.3. For simulation a loss of 0.000000017875 is not really a problem. But, if you do financial calculations millions of times the error 𝜀 will accumulate.

Let’s say we have a very expensive item priced 1 billion dollar for each unit, which is actually not uncommon. We buy 0.1 unit and later 0.2 unit. The accummulation of error is 17.875. So the seller will lose around 17.88 dollar in every transaction. And you don’t want that headache of balancing that on your accounting ledger.

Never use floating point number to represent currency or money.

Conclusion

Floating point is used a lot in scientific notation. It’s very useful and ubiquitous in gaming and simulation. The understanding on how floating point is representation of memory helps us understand why it cannot be used to represent value of money.