Under The Bonnet: Binary Representation of Integer

Demystifying Representation Of Your Data In Computer

Binary Math
If you’re educated in computer science and computer architecture in a legit university, you might have known this. However, not many have that privilege. Many of todays developers are born out of bootcamp, classes, or workshops in which does not teach you how computer really works. It’s okay for certain situation but in one point of time it’ll be an impediment as some problem domain needs that, especially in data communication, security, and IoT.
I have an experience when I interviewed a Java developers who have written many business apps but have no clue what is the result of 2 xor 3 and had no idea that SHA-256 hash is just a representation of a really big integer with 256-bit wide. In interview, this is usually my fizz-buzz test of knowing if a developer understands bitwise operator or not. If they do not and they claim they know security or IoT, I know that’s not true.
Computers Has No Data Type
That’s the first fact you’d need to sink it in. Computer has no data type. It has no concept of integer, floating point or anything. It only understand two things: something getting HIGH or something getting LOW. It can be current or voltage depends on transistor used. But in essence it only understand those two states. To represent those two states we’re representing them with zero (0) and one (1) and we call them bit.
Bit by itself is pretty useless, so we add some more bits to make them a little bit useful. The closest analogy if this will be bits huddled together to an array placed in specific memory location.

8-Bit array and its address in memory
This bit array has 8-bit in size. It’s saved on address 0 to address 7. The address zero is the lowest memory address and address 7 is the highest memory address. Any kind of data can be represented in 0s and 1s and we call them binary. Binary data is opaque, it can be anything. We just know that the memory is filled by bits and it’s up to us to interpret those bits for our own purpose.
Binary Numbering System
Computers were made to do computation. There must be something to do with numbers. Computers only understand low (0) and high (1). We need some way to convert them to the number we understand. Numbers is one of the primary interpretation of those bit array.
We count from 0 to 9 and when we increment 9 we reset the digits to 0 again and add one more digit in the front : 10. This is called base-10 or decimal from latin word decem which means ten and the way we put reset the digit and add more digit in the left is called positional notation.
The reason of using base-10 was due to we’re having ten fingers. Computers do not have ten fingers, and only recognise high and low represented by number 0 and 1. We can still use the same notation with a little bit twist, we add digits when the number reaches two instead of ten.

Decimal vs Binary
Every digit of the number expresses the exponent of the base used. For example the number thirteen is expressed in decimal as 13 and in binary as 1101.
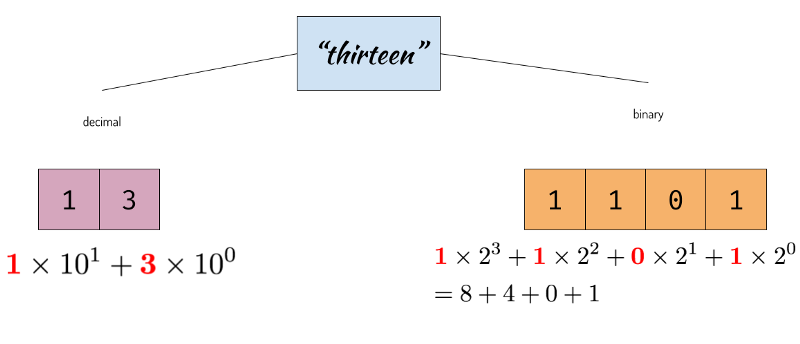
Representing Thirteen in Decimal and Binary
So here we are, we can convert from base-10 to base-2 and vice versa. The arithmetic is still the same but done in base 2. The rightmost digit is called least significant bit (LSB) and the leftmost digit is called most significant bit (MSB). We’ll learn why this is important shortly. This is how numbers are represented in computer memory as binary digits.
There’s one little problem tho: how we store it in computer memory. Do we put LSB on the lowest memory address or highest memory address? This is where things get a little bit tricky because both are correct, there’s no standard body defining on how to store those digits in memory.
Endianess
There are two ways of storing binary digits in memory:
- Increasing numeric significance with increasing memory addresses. It’s called little endian.
- Decreasing numeric significance with increasing memory addresses. it’s called big endian.
Let’s store our number ‘13’ to a hypothetical little and big endian computers.
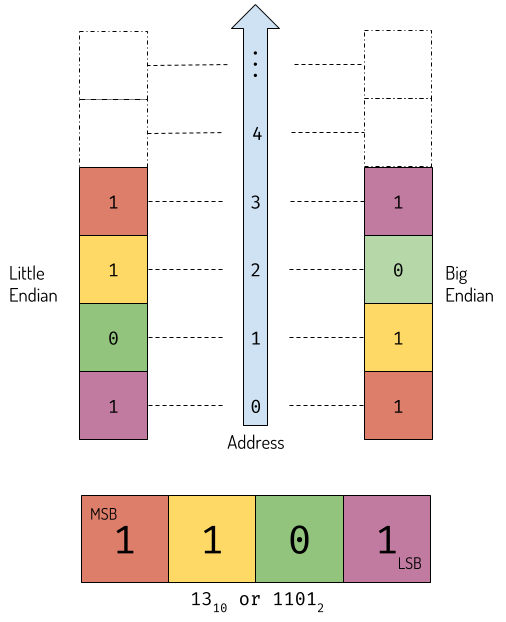
Data representation of number in memory
Processors like Intel is little-endian, and some like IBM’s POWER is big endian. Some other processors like ARM, MIPS, SPARC, etc can be configured to be big or little endian. The data sent over network, according to internet standard RFC-1700 is big endian. Therefore if you have little-endian processor and want to send the bits over the network, you’d need to swap the bits.
In the example above, the minimum number of bits to express 13 is 4. Therefore it’s imperative that machine which can load and save 4-bit at once can process this information easily. The machine capable to do that may be called 4-bit machine. A 32 bit machine can process 32-bit information at once and 64-bit machine can process 64-bit information at once.
Hexadecimal
When discussing about binary. It feels incomplete without also discussing about hexadecimal. Representing a relatively big number is such an hassle when written in binary. However, converting it to decimal also does not solve the problem as there’s no 1–1 mapping of digits between decimal to binary. We can’t determine quickly the size of the information.
Meet hexadecimal. As the name says, it’s base-16 numbering system. The symbols are 0-9and continued with A B C D E F. 16 is 2⁴, therefore each digit in hexadecimal is mapped exactly to four bits maximum. This is very convenient when representing data inside memory of CPU. It’s common to use 0x prefix to represent hexadecimal number. 13 is 0xD and 20 is 0x14.

Decimal, Binary and Hexadecimal
While decimal and binary adds digits in different places, binary and hexadecimal both add one digit at the multiplication of 16 (2⁴). Let’s compare how we convert binary to hexadecimal and decimal.
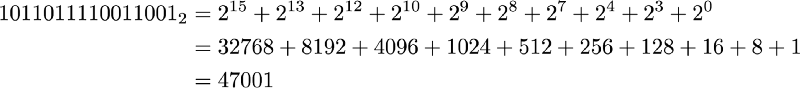
Converting binary to decimal
The result 47001 doesn’t say anything about the original bit. Binary and decimal do not come along. Meanwhile, converting back and forth between binary and hexadecimal is a breeze. Just group the binary digit to 4 bits per group.
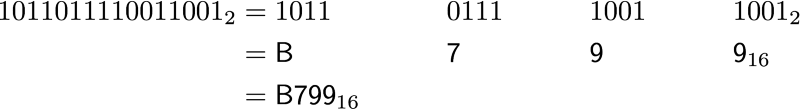
Binary to Hexadecimal
The hexadecimal notation is very popular on expressing binary data, addresses, etc. It’s very convenient.
Byte
Even if computer works in bits, it’s actually hidden to us. The smallest addressable unit of a computer is called a byte. A byte is usually 8 bits representing value of 0–255, or conveniently, in hexadecimal, 0x00to 0xFF. This way, we can group our binary representation to 8 bit each. From this point forward, we will use byte as the unit and hexadecimal value to show the value of each byte.
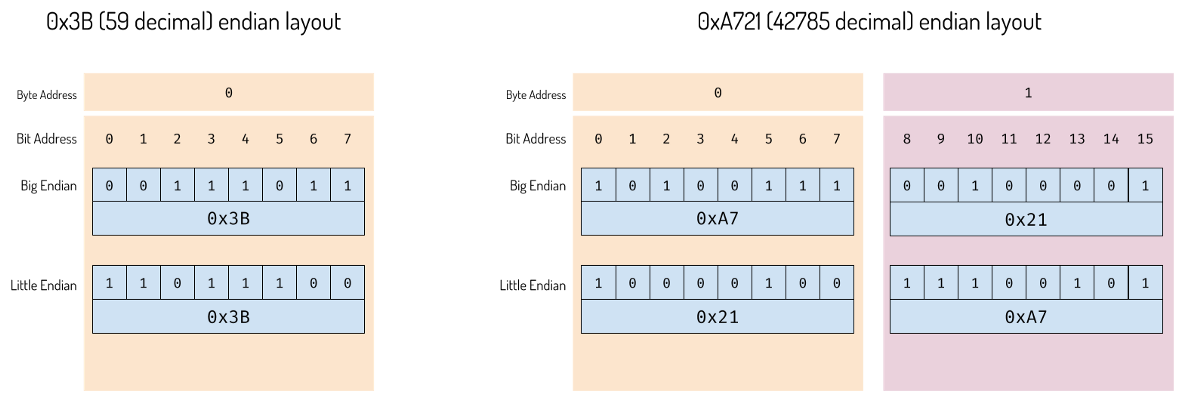
Byte and bits layout
As you can see in the picture above, the difference in endian does not affect single byte. It affects multiple byte information.
The example I was using until this point hasn’t use any negative number at all. Whole numbers with no negative number is called unsigned integers. Up until now it’s what we’re doing. The range of unsigned integer is the same with the width of the processor. For 16-bit processor, we can process an unsigned integer from 0 to 65535 at once.
Expressing Sign
We need to somehow be able to express negative sign. To do that we need to change our interpretation of the bit little bit differently. The common way to encode signed integer is using something called two’s complement. Here’s the rule: > To express negative number, flip all the bits and add one.
The first bit will be the sign bit. If it’s 1 the number is negative if it’s zero the number is positive one.
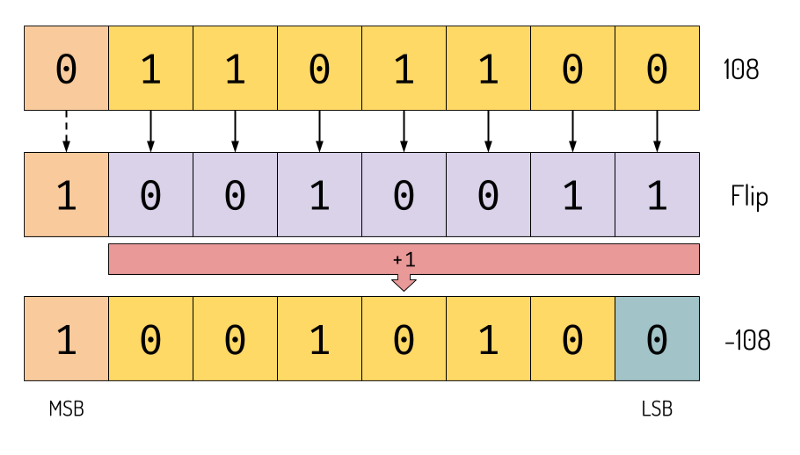
Creating negative number
We repurpose 1 bit in the MSB so the range will change to -127–128.
Testing It In Python
To prove this, we can use small python program to write to the file and then read them using hex editor to see the representation in the memory. Python has package struct with will help us write the binary representation. We’ll use Hex editor like XVi32 or HexFiend, Vim + xxd, or just use online hex editor like hexed.it . We’ll be working with 16-bit integer both signed and unsigned
#!/usr/bin/env pythonimport structnum = 42785
nux = 108f = open("binary.bin", "wb")buf = struct.pack("<H", num)f.write(buf)buf = struct.pack(">H", num)f.write(buf)buf = struct.pack("<h", nux)f.write(buf)buf = struct.pack(">h", nux)f.write(buf)buf = struct.pack("<h", -nux)f.write(buf)buf = struct.pack(">h", -nux)f.write(buf)f.close()
This program will write 42785, 108, and -108 to file named binary.bin . The letter < and > signify little and big endian respectively. If we create the byte array manually the result will be
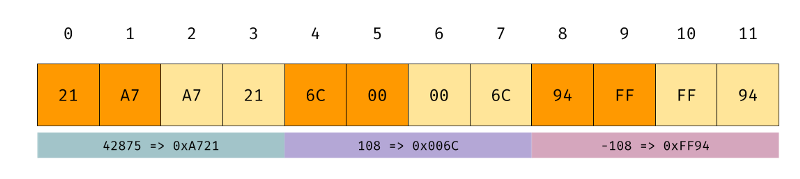
We create the bit array ourselves; orange is little endian; light orange is big endian.
Let’s examine if it’s correct or not by examining the byte array in the hex editor.
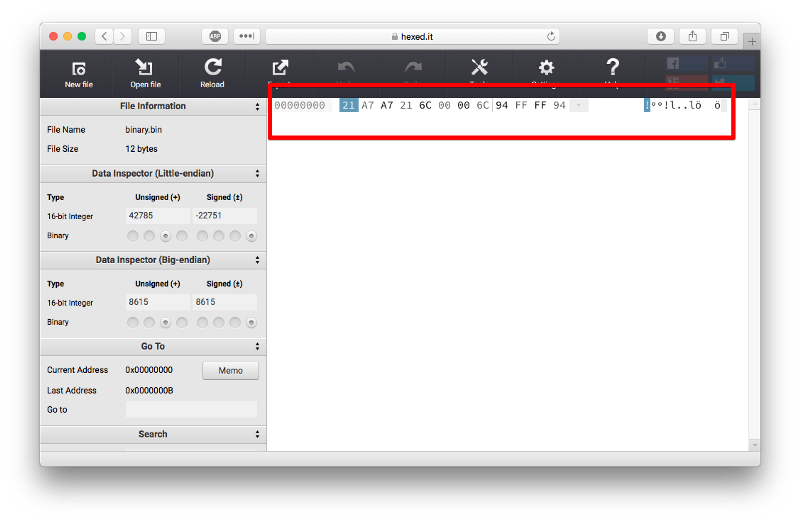
The result of our file in hex editor
As we can see, the result is similar. We can move the cursor to see if the byte array is indeed correct.
Big Integer
The biggest integer that can fit in a register of processor at once nowadays is normally 32-bit or 64-bit. RSA uses 1024-bits integer to do calculation, a secure diffie-hellman exchange needs a big enough prime, usually 1024 or 2048 bit.
So how we represent this? Well, we can still use the same techniques we’ve been used but we take 128 bytes at once. Let’s start with smaller number first, a 128-bit unsigned integer, the same length used by MD5 hash algorithm and UUID.
First, we need to agree on the endian we’ll be using. As we’re not restricted by the native endianess of the CPU, we can choose either. Java uses big endian to represent BigInteger . OpenSSL also uses big endian encoding. So let’s use big endian for now.
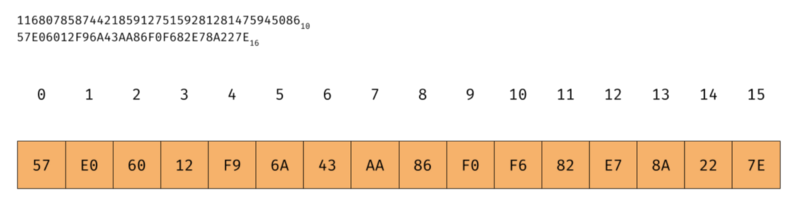
Big integer representation in memory (big-endian encoded)
Test it in Java
As we know that the encoding of Java BigInteger is in big endian according to Java’s own documentation, we can create an array of byte and create big integer out of it. The most significant byte of big-endian is in the lowest address. Lowest address in an array is in the index 0.
import java.math.BigInteger;`public class BigIntegerTester
{
public static void main(String[] args)
{
//57E06012F96A43AA86F0F682E78A227E16
final byte[] data = {
(byte) 0x57, (byte) 0xE0, (byte) 0x60, (byte) 0x12,
(byte) 0xF9, (byte) 0x6A, (byte) 0x43, (byte) 0xAA,
(byte) 0x86, (byte) 0xF0, (byte) 0xF6, (byte) 0x82,
(byte) 0xE7, (byte) 0x8A, (byte) 0x22, (byte) 0x7E};
final BigInteger bi = new BigInteger(data);
System.out.println(bi);
}
}`
The above program will output
116807858744218591275159281281475945086
Yep, that’s our number.
Conclusion
Understanding how informations represented in our computer is valuable knowledge. Binary is not “magic”. It’s just simple representation of information within your computer. Understanding it is essential to implement things like cryptography or data communication. In the next article we’ll talk about character and string representation.


